少し前に半加算器の特徴と回路図という記事を書きました。今回は、その続編ということで全加算器についてまとめていきたいと思います。
1. 全加算器とは?
半加算器は1bitどうしの加算でしたね。しかし、実際に2進数の加算をするときは、下位からの桁上がりを含めて3つの1bitを加算する必要があります。そんな計算をする回路が全加算器です。
2. 真理値表は?論理式は?
真理値表や論理式を導く前に1bitを3つ加算するパターンがいくつあるかみてみます。
①0+0+0=0
②0+0+1=1
③0+1+0=1
④0+1+1=1とCARRY
⑤1+0+0=1
⑥1+0+1=0とCARRY
⑦1+1+0=0とCARRY
⑧1+1+1=1とCARRY
と8つのパターンがあることがわかりました。
ここで、入力(被加算数と加算数と下位からの桁上がり)をそれぞれ「A」,「B」,「carry_in」とし、出力(和と桁上がり)をそれぞれ「SUM」,「carry_out」として下に真理値表を作成します。
| carry_in | B | A | SUM | carry_out |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
上記の真理値表からSUMとcarry_outを論理式で表すと
SUM = A ⊕ B ⊕ carry_in
carry_out = A*carry_in + B*carry_in + A*B
となります。ここでは「⊕」をEXOR, 「+」をOR, 「*」をANDとしています。
3. どんな構成?回路図は?
上記で求めた論理式より、2つのEXOR、3つのAND、2つのORで作れます。
・入力は足す数、足される数、桁上がりの3つです。
・出力は半加算器と同様で和(SUM)と桁上がり(CARRY)の二つです。
その回路図は下のようになります。
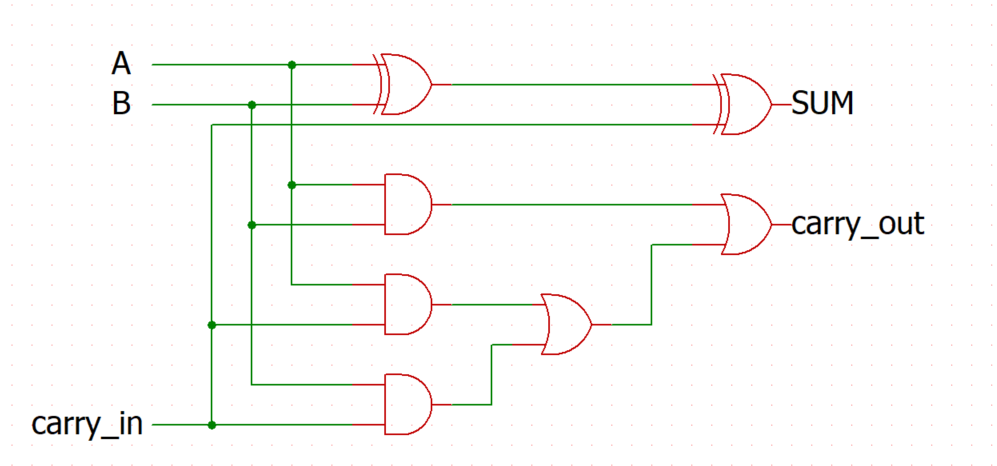
4. 半加算を使用した場合の全加算器
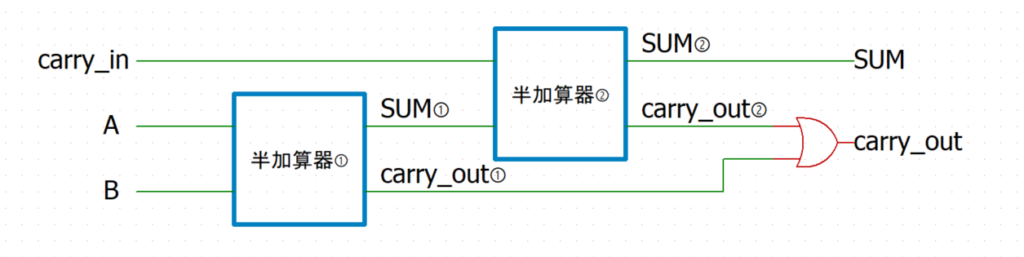
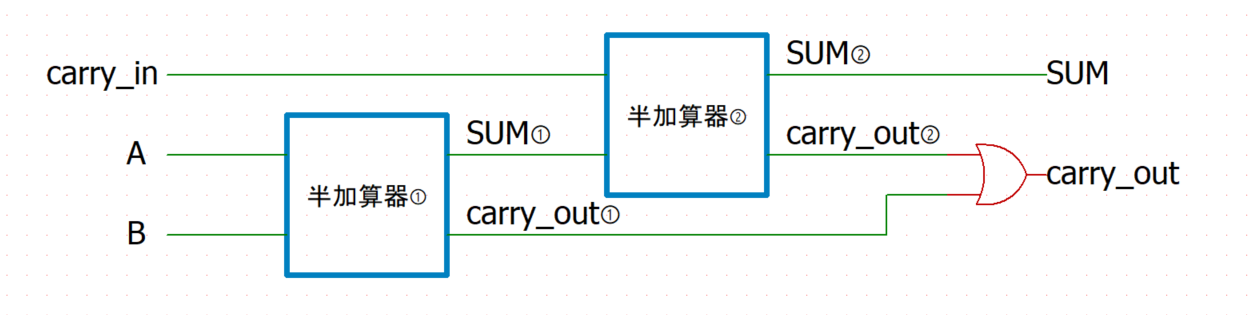
また、全加算器は2つの半加算器と1つのOR回路で作ることもできます。
半加算器を使う構成で考えるとAND素子を一つ節約できることや、回路図を簡素化できるといったメリットがあります。
半加算器①の出力をSUM①とcarry_out①、半加算器②の出力をSUM②とcarry_out②とすると、
回路図は下記のようになります。
ここでは割愛しますが真理値表を用いることで半加算器を使う場合と使わない場合が等価であることが証明できるかと思います。


コメント