論理回路(デジタル回路)にて微分を行う、つまりビット演算ではどのように微分をすればよいかをまとめていきます。
例えば、アナログ信号をAD変換し、デジタルで処理を行うときよくある関数の形にあてはまらないときがほとんどです。しかし、そんな値を微分したい。そんなときに使うのが数値微分というものです。
また、論理回路にて微分を行うにはこの数値微分を用いると良いと思います。
まず、数値微分とは何か。
関数fに対して、なんたらかんたらと教科書等には難しい説明があると思いますが、ここでは省略します。
とりあえず数値微分を一言で、下記の一般式で定義されているのが数値微分です。

その一般式に対してテイラー展開を用いて考えられたのが前方差分と後方差分という微分法です。(微分法という表現が合っているかはわかりませんが)
それぞれの一般式は以下のようになります。
前方差分
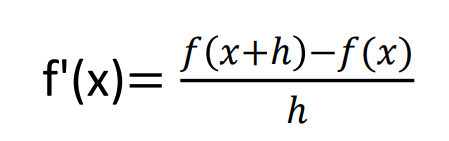
後方差分

今回の例では、後方差分を用いて微分の論理回路図とverilog記述をしてみようと思います。
後方差分の式からh=1としたときに、f(x)-f(x-1)となります。つまり、アナログの波形グラフを考えたときに横軸(x)を時間として、xと(x-1)の関係は、現在の値とその一つ前の関係ということになります。
その関係さえわかれば後は簡単ですよね。現在の入力値と、FFで一段たたいた入力値(つまり1つ前の値)を引いてしまえば良いだけです。
その回路図をしたに描いてみます。

はい、単純ですね。
この微分回路をVerilogHDLで記述すると下記のようになるかと思います。(信号宣言と演算ブロックのみ記載)
input clk;
input in_data;
output out_data;
reg reg_data;
always @(posedge clk)
reg_data <= in_data;
assign out_data = in_data – reg_data;
これで微分したことになると思います。


コメント